This chapter looks at what is involved in discovering a lookup service/service locator. This is common to both services and clients.
A client locates a service by querying a lookup service (service locator). In order to do this, it must first locate such a service. On the other hand, a service must register itself with the lookup service, and in order to do so it must also first locate a service.
The initial phase of both a client and a service is thus discovering a lookup service. Such a service (or set of services) will usually have been started by some independent mechanism. The search for a lookup service can be done either by unicast or by multicast. In fact, the lookup service is just another Jini service, but it is one that is specialised to store services and pass them on to clients looking for them.
Sun supplies a lookup service called reggie as
part of the standard Jini distribution. The specification of a
lookup service is public, and in future we may expect to see
other implementations of lookup services. There may be any
number of these lookup services running in a network. A LAN
may run many lookup services to provide redundancy in case one
of them crashes. Across the internet, people may run lookup
services for a variety of reasons: sometimes a public lookup
service is running on
http://www.jini.monash.edu.au to aid people
trying Jini clients and services without needing to also set
up a lookup service. Other lookup services may act as
co-ordination centres, for example by acting as a repository
of locations for all of the atomic clock servers in the world.
Anybody can start a lookup service (depending on access permissions), but it will usually be started by an administrator, or started at boot time.
Starting a lookup service used to be the hardest part of getting Jini
working for the beginner. It could take hours, or even days of playing
with configuration files and network settings.
It has now been made substantially easier -
just run a DOS batch file or Unix shell script. At the top level of the Jini
distribution is a directory installverify.
Change to this directory and run the program
LaunchAll and it will start an HTTP server, a lookup
service reggie and several other useful services.
For the curious, LaunchAll uses the ServiceStarter
described in a later chapter, and this uses a configuration file
startAll.config. Configuration files will also be described
in a later chapter.
Unicast discovery can be used when you already know the machine on which the lookup service resides, so you can ask for it directly. This is expected to be used for a lookup service that is outside of your local network, which you know the address of anyway (your home network while you are at work, given in some newsgroup or email message, or maybe even advertised on TV!).
The class LookupLocator in package
net.jini.core.discovery is used for this. There
are two constructors,
package net.jini.core.discovery;
public class LookupLocator {
LookupLocator(java.lang.String url) throws
java.net.MalformedURLException;
LookupLocator(java.lang.String host,int port);
}
jini://host/ or
jini://host:port/. If no port is given, it
defaults to 4160. The host should be a valid DNS name (such as
www.jini.monash.edu.au or an IP address (such as
137.92.11.13). No unicast discovery is performed
at this stage, though, so any rubbish could be entered. Only a
check for syntactic validity of the URL is performed. This
syntantic check is not even done for the second constructor.
The following program creates some objects with valid and invalid host/URLs. They are only checked for syntactic validity rather than existence as URLs:
package basic;
import net.jini.core.discovery.LookupLocator;
/**
* InvalidLookupLocator.java
*/
public class InvalidLookupLocator {
static public void main(String argv[]) {
new InvalidLookupLocator();
}
public InvalidLookupLocator() {
LookupLocator lookup;
// this is valid
try {
lookup = new LookupLocator("jini://localhost");
System.out.println("First lookup creation succeeded");
} catch(java.net.MalformedURLException e) {
System.err.println("First lookup failed: " + e.toString());
}
// this is probably an invalid URL,
// but the URL is syntactically okay
try {
lookup = new LookupLocator("jini://ABCDEFG.org");
System.out.println("Second lookup creation succeeded");
} catch(java.net.MalformedURLException e) {
System.err.println("Second lookup failed: " + e.toString());
}
// this IS a malformed URL, and should throw an exception
try {
lookup = new LookupLocator("A:B:C://ABCDEFG.org");
System.out.println("Third lookup creation succeeded");
} catch(java.net.MalformedURLException e) {
System.err.println("Third lookup failed: " + e.toString());
}
// this is valid, but no check is made anyway
lookup = new LookupLocator("localhost", 80);
System.out.println("Fourth lookup creation succeeded");
}
} // InvalidLookupLocator
All programs in this book can be compiled using the JDK 1.2
compiler. Jini programs will not compile or run under JDK 1.1
(any versions). The Java 1.5 compiler can be used, although
the Jini class libraries do not
use any of the 1.5 features. The following program defines the class
InvalidLookupLocator in package
basic. The source code will in the file
InvalidLookupLocator.java in the
basic subdirectory. From the parent directory,
this can be compiled by a command such as
javac basic/InvalidLookupLocator.java
basic
subdirectory.
The CLASSPATH will need to include some Jini jar files.
In versions 2.0 and earlier the
jini-core.jar jar was required.
This has changed for Jini 2.1 - the preferred files are
jsk-platform.jar and jsk-lib.jar
for compilation of the source code. These files are in the
lib subdirectory of the Jini distribution.
When a service is run, these Jini files will need to be in its
CLASSPATH. Similarly, when a client runs, it will
also need these files in its CLASSPATH. The reason
for this repetition is that the service and the client are two
separate applications, running in two separate Java Virtual
Machines, and quite likely will be on two separate computers.
The InvalidLookupLocator has no additional
requirements. It does not perform any network calls, and does
not require any additional service to be running. So it can be
run simply by
java -Djava.security.policy=policy.all -classpath ... basic.InvalidLookupLocator
grant { permission
java.security.AllPermission;
};
An Ant file to build, deploy and run this class is
A LookupLocator has methods
String getHost();
int getPort();
Search and lookup is performed by the method
getRegistrar() of the LookupLocator
which returns an object of class
ServiceRegistrar.
public ServiceRegistrar getRegistrar() throws
java.io.IOException,
java.lang.ClassNotFoundException
ServiceRegistrar
is discussed in detail later. This performs network lookup on
the URL given in the LookupLocator constructor.
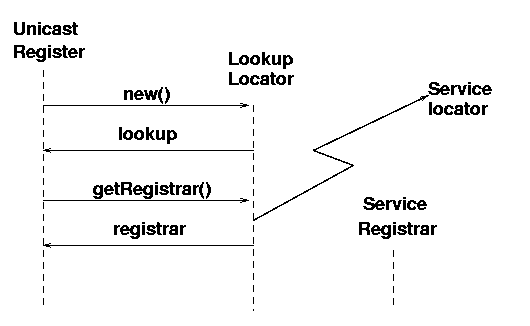
UML sequence diagrams are useful for showing the timelines of object
existence and the method calls that are made from one object
to another. The timeline reads down, and method calls and
their returns read across. A UML sequence diagram augmented
with a jagged arrow showing the network connection is shown in
figure 4.1. The
UnicastRegister object makes a new()
call to create a LookupLocator and this call
returns a lookup object. The method call
getRegistrar() is then made on the
lookup object, and this causes network activity.
As a result of this, a ServiceRegistrar object is
created in some manner by the lookup object, and
this is returned from the method as the
registrar.

package basic;
import net.jini.core.discovery.LookupLocator;
import net.jini.core.lookup.ServiceRegistrar;
import java.rmi.RMISecurityManager;
/**
* UnicastRegistrar.java
*/
public class UnicastRegister {
static public void main(String argv[]) {
new UnicastRegister();
}
public UnicastRegister() {
LookupLocator lookup = null;
ServiceRegistrar registrar = null;
System.setSecurityManager(new RMISecurityManager());
try {
lookup = new LookupLocator("jini://localhost");
} catch(java.net.MalformedURLException e) {
System.err.println("Lookup failed: " + e.toString());
System.exit(1);
}
try {
registrar = lookup.getRegistrar();
} catch (java.io.IOException e) {
System.err.println("Registrar search failed: " + e.toString());
System.exit(1);
} catch (java.lang.ClassNotFoundException e) {
System.err.println("Registrar search failed: " + e.toString());
System.exit(1);
}
System.out.println("Registrar found");
// the code takes separate routes from here for client or service
}
} // UnicastRegister
registrar object will be used in different
ways for clients and services: the services will use it to
register themselves, and the clients will use it to locate
services.
The program needs to be compiled and run with
jsk-platform.jar and jsk-lib.jar
in its CLASSPATH.
javac -classpath ... basic/UnicastRegister.java
localhost. It could, however, be any machine
accessible on the local or remote network (as long as it is
running a service locator). For example, sometimes a
service locator is running on my current workstation,
jan.newmarch.name. The
parameter to LookupLocator would be
jini://jan.newmarch.name.
This program will receive a ServiceRegistrar from
the service locator. However, it does so by a simple
readObject() on a socket connected to the service
locator, and so does not need any additional support services
such as rmiregistry or rmid. It can
be run by
java -Djava.security.policy=policy.all -classpath ... basic.UnicastRegister
An Ant file to build, deploy and run this class is
If the location of a lookup service is unknown, it is necessary to make a broadcast search for one. UDP supports a multicast mechanism which the current implementations of Jini use. Because multicast is expensive in terms of network requirements, most routers block multicast packets. This usually restricts broadcast to a local area network, although this depends on the network configuration and the time-to-live (TTL) of the multicast packets.
There may be any number of lookup services running on the network accessible to broadcast search. On a small network, such as a home network, there may be just a single lookup service, but in a large network there may be many - perhaps one or two per department. Each one of these may choose to reply to a broadcast request.
Some services may be meant for anyone to use, but some may be more restricted in applicability. For example, the Engineering Dept may wish to keep lists of services specific to that department. This may include a departmental diary service, a deparmental inventory, etc. The services themselves may be running anywhere in the organisation, but the department would like to be able to store information about them and to locate them from their own lookup service. Of course, this lookup service may be running anywhere too!
So there could be lookup services specifically for a particular group of services such as the Engineering Dept services, and others for the Publicity Dept services. Some lookup services may cater for more than one group - for example a company lookup service may want to hold information about all services running for all groups.
When a lookup service is started, it can be given a list of groups to act for as a command line parameter. A service may include such group information by giving a list of groups that it belongs too. This is an array of strings, such as
String [] groups = {"Engineering dept"};
The class LookupDiscovery in package
net.jini.discovery is used for broadcast
discovery. There are two constructors
LookupDiscovery(java.lang.String[] groups)
LookupDiscovery(java.lang.String[] groups, Configuration config)
The parameter to the first LookupDiscovery constructor
can take three cases
null, or
LookupDiscovery.ALL_GROUPS,
means to attempt to discover all reachable lookup services
no matter which group they belong to.
This will be the normal case.
An empty list of strings, or
LookupDiscovery.NO_GROUPS,
means that the object is created, but no search is performed. In this
case, the method setGroups() will need to be
called
in order to perform a search.
A non-empty array of strings can be given. This will attempt to discover all lookup services in that set of groups.
A broadcast is a multicast call across the network, expecting
lookup services to reply as they receive it. Doing so may take
time, and there will generally be an unknown number of lookup
services that can reply. To be notified of lookup services as
they are discovered, the application must register a listener
with the LookupDiscovery object.
public void addDiscoveryListener(DiscoveryListener l)
DiscoveryListener interface:
package net.jini.discovery;
public abstract interface DiscoveryListener {
public void discovered(DiscoveryEvent e);
public void discarded(DiscoveryEvent e);
}
The discovered() method is invoked whenever a
lookup service has been discovered. The API recommends that
this method should return quickly, and not make any remote
calls. However, for a service it is the natural place to
register the service, and for a client it is the natural place
to ask if there is a service available and to invoke this
service. It may be better to perform these lengthy operations
in a separate thread.
There are other timing issues involved: when the
DiscoveryListener is created, the broadcast is
made. After this, a listener is added to this discovery
object. What happens if replies come in very quickly, before
the listener is added? The ``Jini Discovery Utilities
Specification'' guarantees that these replies will be buffered
and delivered when a listener is added. Conversely, no replies
may come in for a long time - what is the application supposed
to do in the meantime? It cannot simply exit, because then
there would be no object to reply to! it has to be made
persistent enough to last till replies come in. One way of
handling this is if the application has a GUI interface - then
it will stay till the user dismisses it. Another possibility
is that the application may be prepared to wait for a while
before giving up. In that case the main could sleep for, say,
ten seconds and then exit. This will depend on what the
application should do if no lookup service is discovered.
The discarded() method is invoked whenever the
application discards a lookup service by calling
discard() on the registrar object.
The parameter to the discovered()method of the
DiscoveryListener interface is a
DiscoveryEvent object.
package net.jini.discovery;
public Class DiscoveryEvent {
public net.jini.core.lookup.ServiceRegistrar[] getRegistrars();
}
getRegistrars() which returns an array of
ServiceRegistrar objects. Each one of these
implements the ServiceRegistrar interface, just
like the object returned from a unicast search for a lookup
service. More than one can be returned if a set of replies
have come in before the listener was registered - they are
collected in an array and returned in a single call to the
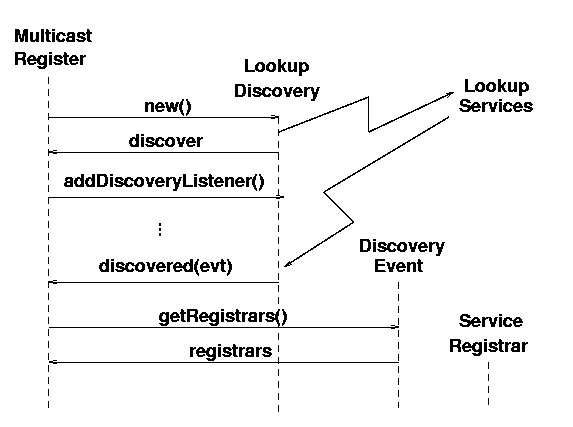
listener. A UML sequence diagram augmented with jagged arrows
showing the network broadcast and replies is shown in figure
4.2.
In this figure, creation of a LookupDiscovery object
starts the broadcast search, and it returns the
discover object. The
MulticastRegister adds itself as listener to the
discover object. The search continues in a
separate thread, and when a new lookup service replies, the
discover object invokes the
discovered() method in the
MulticastRegister, passing it a newly created
DiscoveryEvent. The
MulticastRegister object can then make calls on
the DiscoveryEvent such as
getRegistrars(), which will return suitable
ServiceRegistrar objects.
By this stage the program looks like
package basic;
import net.jini.discovery.LookupDiscovery;
import net.jini.discovery.DiscoveryListener;
import net.jini.discovery.DiscoveryEvent;
import net.jini.core.lookup.ServiceRegistrar;
import net.jini.core.discovery.LookupLocator;
import java.rmi.RemoteException;
/**
* MulticastRegister.java
*/
public class MulticastRegister implements DiscoveryListener {
static public void main(String argv[]) {
new MulticastRegister();
// stay around long enough to receive replies
try {
Thread.currentThread().sleep(10000L);
} catch(java.lang.InterruptedException e) {
// do nothing
}
}
public MulticastRegister() {
System.setSecurityManager(new java.rmi.RMISecurityManager());
LookupDiscovery discover = null;
try {
discover = new LookupDiscovery(LookupDiscovery.ALL_GROUPS);
} catch(Exception e) {
System.err.println(e.toString());
e.printStackTrace();
System.exit(1);
}
discover.addDiscoveryListener(this);
}
public void discovered(DiscoveryEvent evt) {
ServiceRegistrar[] registrars = evt.getRegistrars();
for (int n = 0; n < registrars.length; n++) {
ServiceRegistrar registrar = registrars[n];
// the code takes separate routes from here for client or service
try {
System.out.println("found a service locator at " +
registrar.getLocator().getHost() +
" at port " +
registrar.getLocator().getPort());
} catch(RemoteException e) {
e.printStackTrace();
}
}
}
public void discarded(DiscoveryEvent evt) {
}
} // MulticastRegister
In the constructor we create a LookupDiscovery
object, add a DiscoveryListener and then the
constructor terminates. The main() method, having
called this constructor, promptly goes to sleep. What is going
on here? The constructor to LookupDiscovery
actually starts up a number of threads, to broadcast the
service and to listen for replies. (See the chapter on Architecture). When replies come
in, the listener thread will call the
discovered() method of the
MulticastRegister. However, these threads are
daemon threads. Java has two types of
threads: daemon and user threads, and at least one user thread
must be running or the application will terminate. All these
other threads are not enough to keep the application alive,
and it keep a user thread running in order to continue to
exist.
The sleep() ensures that a user thread continues
to run, even though it apparently does nothing! This will keep
the application alive so that the daemon threads (running in
the ``background'') can discover some lookup locators. Ten
seconds (10,000 milliseconds) is long enough for that. To stay
alive after this ten seconds expires will
depend on either increasing the sleep time or creating another
user thread in the discovered() method. Later in
this book, use is made in ``leasing'' of a useful constant
Lease.FOREVER. While the ``leasing'' system
understands a special meaning for this constant, the standard
Java sleep() merely uses its value
Long.MAX_VALUE and just sleeps for a lengthy
period.
I have placed the sleep() in the
main() method. It is perfectly reasonable to
place it in the application constructor, and some examples do
this. However, it looks a bit strange there, so I prefer this
placement. Note that although the constructor to
MulticastRegister will have terminated without us
assigning its object reference, a live reference has been
passed into the discover object as a
DiscoveryListener and it will keep the reference
alive in its own daemon threads. This means that the
application object will still exist for its
discovered() method to be called.
Any other method that results in a user thread continuing to exist will do just as well. For example, a client that has an AWT or Swing user interface will stay alive because there are many user threads created by any of these GUI objects.
For services, which typically will not have a GUI interface
running, another simple way is to create an object and then
wait for another thread to notify() it. Since
nothing will, the thread (and hence the application) stays
alive. Essentially, this is an unsatisfied wait that will
never terminate - usually an erroneous thing to do, but here
it is deliberate.
Object keepAlive = new Object();
synchronized(keepAlive) {
try {
keepAlive.wait();
} catch(InterruptedException e) {
// do nothing
}
}
sleep() which will terminate
eventually.
The program needs to be compiled and run with
jsk-platform.jar and jsk-lib.jar
in its CLASSPATH.
javac -classpath ... basic/MulticastRegister.java
java -Djava.security.policy=policy.all -classpath ... basic.MulticastRegister
This program will receive ServiceRegistrar's from
the service locators. However, it does so by a simple
readObject() on a socket connected to a service
locator, and so does not need any additional support services
such as rmiregistry.
An Ant file to build, deploy and run this class is
Services and clients search for lookup locators using the multicast protocol, by sending out packets as UDP datagrams. It makes announcements on UDP 224.0.1.84 on port 4160. How far do these announcements reach? This is controlled by two things:
the ``time to live'' (TTL) field on the packets
network administrator settings on routers and gateways
LookupDiscovery sets the TTL to be 15. Common
network administrative settings restrict such packets to the
local network. However, the TTL may be changed by giving the
system property net.jini.discovery.ttl a
different value. But be careful about setting this: many
people will get irate if you flood the networks with multicast
packets.
The ServiceRegistrar is an abstract class which is
implemented by each lookup service. The actual details of this
implementation are not relevant here. The
role of a ServiceRegistrar is
to act as a proxy for the lookup service.
This proxy runs in the application, which may be a service or a
client.
This is the first object that is moved from one Java process to
another in Jini. It is shipped from the lookup service to the
application looking for the lookup service, using a socket
connection. From then it runs as an object in the application's
address space, and the application makes normal method calls to
it. When needed, it communicates back to its lookup service. The
implementation used by Sun's reggie uses RMI to
communicate, but the application does not need to know this, and
anyway, it could be done in different ways. This proxy object
should not cache any information on the application side, but
get ``live'' information from the lookup service as needed. The
implementation of the lookup service supplied by Sun does
exactly this.
This object has two major methods, one used by a service attempting to register
public
ServiceRegistration register(ServiceItem item, long leaseDuration)
throws java.rmi.RemoteException
public java.lang.Object lookup(ServiceTemplate tmpl)
throws java.rmi.RemoteException;
public ServiceMatches lookup(ServiceTemplate tmpl, int maxMatches)
throws java.rmi.RemoteException;
A service provider will register a service object (that is, an
instance of a class), and a set of attributes for that object.
For example, a printer may specify that it can handle Postscript
documents, or a toaster that it can deal with frozen slices of
bread. The service provider may register a singleton object that
completely implements the service, but more likely it will
register a service proxy that will communicate back to other
objects in the service provider. Note carefully: the
registered object will be shipped around the network. When it
finally gets to run, it may be a long way away from where it
was originally created. It will have been created
in the service's JVM, transferred to the lookup locator by
register() and then to the client's JVM by
lookup().
A client is trying to find a service, using some properties of
the service that it knows about. Whereas the service can export
a live object, the client cannot use a service object as a
property - because then it would already have the thing, and
wouldn't need to try to find one! What it can do is to use a
class object, and try to find if there are
any instances of this class lying around in
service locators. As discussed later in Client Search, it is best if
the client asks for an interface class object. In
addition to this class specification, the client may specify a
set of attribute values that it requires from the service.
The next step is to look at the possible forms of attribute
values, and how matching will be performed. This is done using
Jini Entry objects. The
simplest services, and the least demanding clients, will not
require any attributes: the Entry[] array will be
null. You may wish to skip ahead to service registration
or to client search and
come back to entries later.
The ServiceRegistrar is returned after a
successful discovery has been made. This object has a number
of methods that will return useful information about the
lookup service itself. So in addition to using this object to
register a service or lookup a service, you can use it to find
out about the lookup locator. The major methods are
String[] getGroups();
LookupLocator getLocator();
ServiceID getServiceID();
getGroups() will return a list of the
groups that the locator is a member of.
The second method, getLocator() is more
interesting. This is exactly the same object as is used in the
unicast lookup, but now its fields are filled in by the
discovery process. So you can find which host the locator is
running on, and its hostname by
registrar.getLocator().getHost();
public void discovered(DiscoveryEvent evt) {
ServiceRegistrar[] registrars = evt.getRegistrars();
for (int n = 0; n < registrars.length; n++) {
ServiceRegistrar registrar = registrars[n];
System.out.println("Service locator at " +
registrar.getLocator().getHost());
}
}
The third method getServiceID() is unlikely to be
of much use to you. In general, service ID's are used to give
a globally identifier for the service (no different services
should have the same ID), and a service should have the same
ID with all service locators. However, this is the service ID
of the lookup service, not of any services registered with it.
Both services and clients need to find lookup services. Discovering a lookup service may be done using unicast or multicast protocols. Unicast discovery is a synchronous mechanism. Multicast discovery is an asynchronous mechanism that requires use of a listener to respond when a new service locator is discovered.
When a service locator is discovered, it sends a
ServiceRegistrar object to run in the client or
service. This acts as a proxy for the locator. This object may
be queried for information, such as the host the service locator
is on.
If you found this chapter of value, the full book "Foundations of Jini 2 Programming" is available from APress or Amazon .
 This work is licensed under a
Creative Commons License, the replacement for the earlier Open Content License.
This work is licensed under a
Creative Commons License, the replacement for the earlier Open Content License.